|
Пример текста Решения задачи
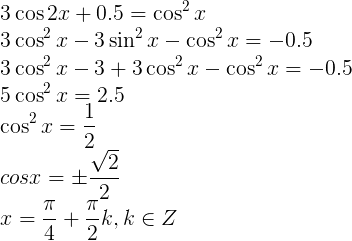
Косинус двойного аргумента (угла)
$ \cos(2x) = \cos^2(x) - \sin^2(x) $ Комментарииcos2x=cos^2x-sin^2x=2cos^2x-1 тогда 3(2cos^2x-1)+0,5=cos^2x 6cos^2x-3+0.5-cos^2x=0 5cos^2x=2.5 cos^2x=0.5=1/2 ____ __ __ cosx=V(1/2)=V(2)/2, где V - квадратный корень x=45 град. Комментарии3cos2x + 0.5 = cos^2x 3cos^2x - 3sin^2x + 0.5 = cos^2x 2cos^2x + 0.5 = 3sin^2x 1+2cos2x + 0.5 = 3 * [(1-cos2x)/2] 2+ 2cos2x +1 =3 - 3cos2x 5cos2x= 0 cos2x = 0 2x = π/2 + π x = π/4 + π/2k формула 1
cos2x = cos^2x - sin^2x формула 2
cos^2x = (1+cos2x) / 2 формула 3
sin^2x= (1-cos2x) / 2 КомментарииЧтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все математики |


Комментарии