Задачи по тригонометрии Активность в теме ТригонометрияСамые активные математики в теме ТригонометрияЛучшие решения в теме ТригонометрияВычислить
Спасибо за ответы. Нужно было решение без использования калькулятора. Вот мой пример решения 
рисунок 1 3cos2x+0,5=cos^2x
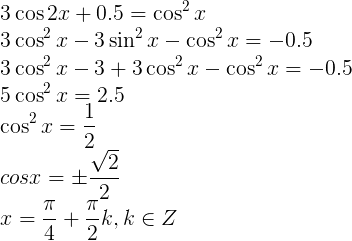
Косинус двойного аргумента (угла)
$ \cos(2x) = \cos^2(x) - \sin^2(x) $ КомментарииВычислить
Практикуем навык владения калькулятором. Вводим задание в необходимом виде, а т.е: формула 1
$ \cos(2*\pi/7)*\cos(3*\pi/7)*\cos(6*\pi/7) $ И получаем: =-1/8=-0.124999 или же примерно 0.13 КомментарииВычислить
Ответ: 0.14 формула 1
$ \frac{2p}{7} = 0.89 $ формула 2
$ \frac{3p}{7} = 1.34 $ формула 3
$ \frac{6p}{7} = 18.84 $ формула 4
$ \cos(0.89) = 0.62 $ формула 5
$ \cos(1.34) = 0.22 $ формула 6
$ \cos(18.84) = 0.99 $ формула 7
$ \cos(0.89) * \cos(1.34) * \cos(18.84) = $ формула 8
$ = 0.62 * 0.22 * 0.99 = 0.13 $ Я бы сказал только около 0.13, ну такой волнистый знак равно. КомментарииОтвет: 0.14 или же ~0.13, как написано ранее?
3cos2x+0,5=cos^2x
cos2x=cos^2x-sin^2x=2cos^2x-1 тогда 3(2cos^2x-1)+0,5=cos^2x 6cos^2x-3+0.5-cos^2x=0 5cos^2x=2.5 cos^2x=0.5=1/2 ____ __ __ cosx=V(1/2)=V(2)/2, где V - квадратный корень x=45 град. КомментарииСложнейшие задачи в теме Тригонометрия Тема задачи: Тригонометрия
решить уравнение (учитель объяснял про перебор корней на круге, но это так сложно, что я не усвоил... Я пытался)
8 февраля 2017 21:27
1 подписчик
1311 просмотр
2
решения Тема задачи: Тригонометрия
3cos2x+0,5=cos^2x
22 февраля 2016 13:53
0 подписчиков
7873 просмотра
3
решения Тема задачи: Тригонометрия
Найти косинус угла
21 июля 2016 16:19
0 подписчиков
1105 просмотров
1
решение Тема задачи: Тригонометрия
Упрощение тригонометрических выражений, желательно с решениями
20 ноября 2022 05:40
0 подписчиков
1162 просмотра
0
решений |
Записать новую задачу Все задачи Все темы Все математики |
Комментарии