Задачи про геометрическую прогрессию Активность в теме Геометрическая прогрессияСамые активные математики в теме Геометрическая прогрессияЛучшие решения в теме Геометрическая прогрессияГеометрическая прогрессия
запишу, что имеем формула 1
$ a_1 + a_3 + a_9 = 78 $ формула 2
$ a_n = a_1 · q^{n−1} $ формула 3
$ a_3 = a_1 · q^2 $ формула 4
$ a_9 = a_1 · q^8 $ формула 5
$ a_1 + a_1 · q^2 + a_1 · q^8 = 78 $ вот получилось такое уравнение, пока думаю, что с ним делать дальше, придумал, продолжаем разговор: формула 6
$ 1 + q^2 + q^8 = \frac{78}{a_1} $ Если считать, что q и a1 - целые натуральные числа, то получается один единственный ответ, который получается подбором - возьмем q=2, a1=1 формула 8
$ q^8 = 256 $ А это значительно больше чем 78, а если принять a1=2, то 256 > 39, тогда остается только принять q = 1. Тогда формула 9
$ 3 = \frac{78}{a_1} $ Отсюда получим формула 10
$ a_1 = \frac{78}{3} = 26, q=1 $ и все члены прогрессии равны формула 11
$ a_1 = a_3 = a_9 = 26 $ А вот если считать, что a1 и q рациональные дробные числа, тогда уравнение задачи имеет бесконечное множество решений которые можно увидеть на графике функции формула 13
$ y(x) = 1 + x^2 + x^8 $ 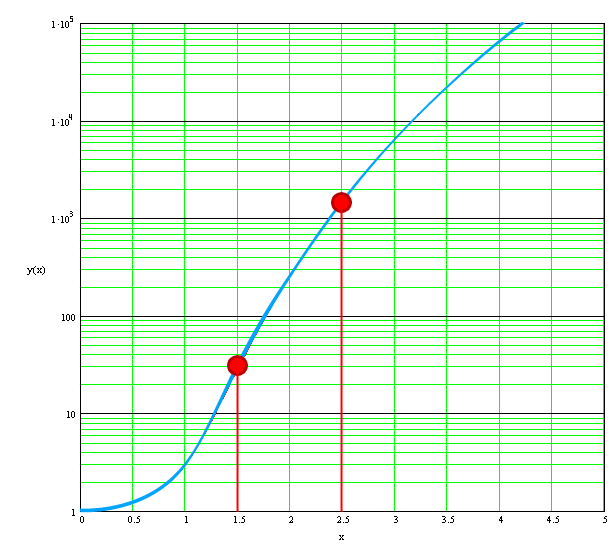
рисунок 1 возьмем q=1.5 формула 14
$ y(q=1.5) = 28.879 = \frac{78}{a_1} $ формула 15
$ a_1 = 2.701 $ Или возьмем q=2.5 формула 16
$ y(q=2.5) = 1533.129 = \frac{78}{a_1} $ формула 17
$ a_1 = 0.051 $ Итого - при целых натуральных a1 и q получаем q=1 a1=26, при рациональных дробных a1 и q получаем бесконечное множество решений Геометрическая прогрессия
Воспользуемся свойством геометрической прогрессии Свойство геом. прогрессии
$ b_{n}^{2} = b_{n-1}b_{n+1} $ Предположим, что b - средний член, тогда: уравнение 1
b^{2} =ac Из условия возьмем 2 других уравнения. уравнение 2
$ a+b+c=26 $ уравнение 3
$ a^{2}+b^{2}+c^{2}=364 $ Имеем систему уравнений. b^2=ac a+b+c=26 a^2+b^2+c^2=364 Решение системы громоздкое, поэтому не привожу ее решения ( если потребуется, могу привести) Решением этой системы будут 2 такие тройки: a=2 b=6 c=18 a=18 b=6 c=2 И произведением будет abc=2*6*18=216 Ответ: 216. КомментарииГеометрическая прогрессия
Три числа, сумма которых равна 78 = a+b+c=78; Их можно рассматривать как первый, третий и девятый члены арифметической прогрессии a=x; b=3x; c=9x; 13x = 78; x =6. Найдите наибольшее из этих чисел a=6; b=18; c=54 54. КомментарииСложнейшие задачи в теме Геометрическая прогрессия Тема задачи: Геометрическая прогрессия
Геометрическая прогрессия Тема задачи: Геометрическая прогрессия
Геометрическая прогрессия
10 декабря 2015 17:28
0 подписчиков
5535 просмотров
2
решения  Тема задачи: Геометрическая прогрессия
Геометрическая прогрессия Тема задачи: Геометрическая прогрессия
Геометрическая прогрессия
10 декабря 2015 17:25
0 подписчиков
2086 просмотров
1
решение |
Записать новую задачу Все задачи Все темы Все математики |











Комментарии