Нет подходящей темы Задачи

Создано: @ichigo 30 января 2016 21:38

поставьте оценку:

2 голосов, средний бал: 5.0000

Рисую рисунок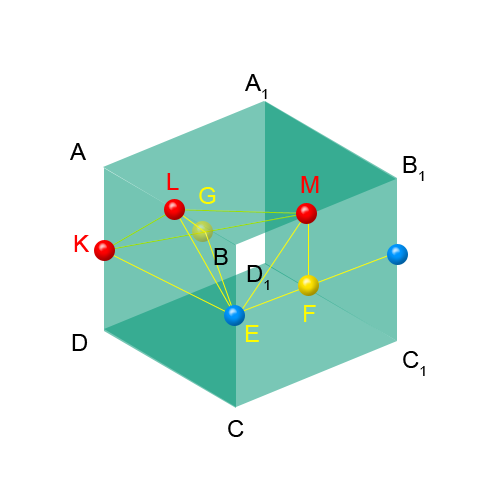

рисунок 1

Нарисовав требуемые середины ребер куба мы видим треугольник из этих точек который принадлежит секущей плоскости KLM. Однако как пойдет плоскость из рисунка не совсем ясно и какие стороны и как она пересечет тоже. Поэтому надо поразмыслить. Я построил дополнительные точки EFG. E - это середина ребра BC. F центр стороны B-B1-C1-C. G середина КМ.

При помощи треугольника KEM мы найдем длину KM. и найдем в треугольнике KLM его углы. Потом найдем KG и GM и при помощи них и треугольников KEM найдем стороны и углы LGE. Вот углы это и есть отправная точка к окончательному решению. но пока отложу его на завтра.

В общем на меня снизошло озарение - это же куб, он симметричный, и если продолжить построение по законам симметрии то получим все точки пересечения с ребрами куба и соответсвено секущую плоскость - которая получилась правильным шестиугольником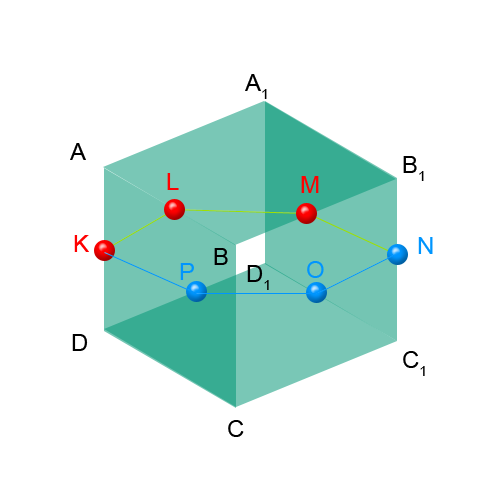

рисунок 2

ответ: секущая плоскость - правильный шестиугольник

Создано: @nick 8 августа 2016 12:06

поставьте оценку:

2 голосов, средний бал: 5.0000

Дано: лодка прошла по течению реки и затем возвращается против течения

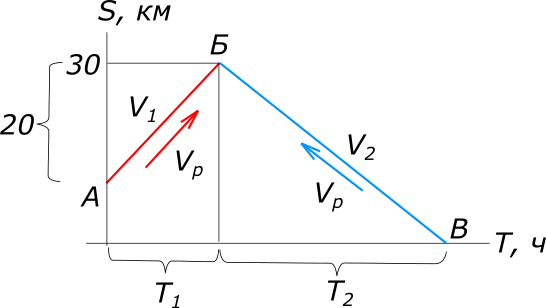
рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{1}+T_{2}=\frac{20}{3}$

$\frac{S_{1}}{V_{1}}+\frac{S_{2}}{V_{2}}=\frac{20}{3}$

$\frac{S_{1}}{V_{л}+V_{р}}+\frac{S_{2}}{V_{л}-V_{р}}=\frac{20}{3}$

$3S_{1}V_{л}-3S_{1}V_{р}+3S_{2}V_{л}+3S_{2}V_{р}=20V_{л}^2-20V_{р}^2$

$20V_{л}^2-3(S_{1}+S_{2})V_{л}-3(S_{2}-S_{1})V_{р}-20V_{р}^2=0$

$V_{л_{1}}=9; V_{л_{1}}=-1,5$

Ответ: собственная скорость лодки 9 км/ч.

Создано: @nick 8 августа 2016 18:51

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: лыжник догоняющий на трассе сначала одного а затем второго соперника

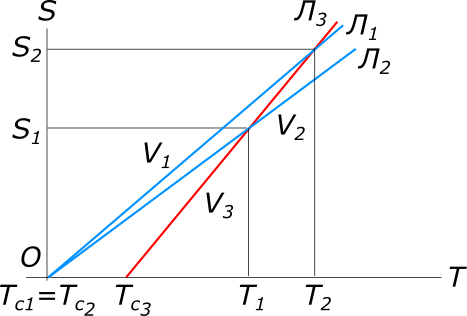
рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнения:

$V_{1}=\frac{7}{6}V_{2}, откуда V_{2}=\frac{6}{7}V_{1}$

Тогда $\frac{\frac{5}{6}V_{3}-\frac{1}{2}\frac{6}{7}V_{1}}{V_{3}-\frac{6}{7}V_{1}}=\frac{\frac{1}{3}V_{3}}{V_{3}-V_{1}}$

$(\frac{5}{6}V_{3}-\frac{1}{2}\frac{6}{7}V_{1})(V_{3}-V_{1})=\frac{1}{3}V_{3}(V_{3}-\frac{6}{7}V_{1})}$

$\frac{5}{6}V_{3}^2-\frac{3}{7}V_{1}V_{3}-\frac{5}{6}V_{3}V_{1}+\frac{3}{7}V_{1}^2=\frac{1}{3}V_{3}^2-\frac{2}{7}V_{3}V_{1}$

$18V_{1}^2-41V_{1}V_{3}+21V_{3}^2=0$

$V_{1_{1}}=27; V_{1_{2}}=14$

Ответ: скорость первого лыжника 14 км/ч.

Создано: @nick 10 августа 2016 08:46

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: две пары золотых слитков

получены сплавы золотых слитков 1, 2 и 3, 4

Ответ: пробы золота 1-ого и 2-ого слитков 56% и 66% соответственно.

Создано: @nick 8 августа 2016 10:08

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: катер плывет по течению реки вниз и затем возвращается против течения

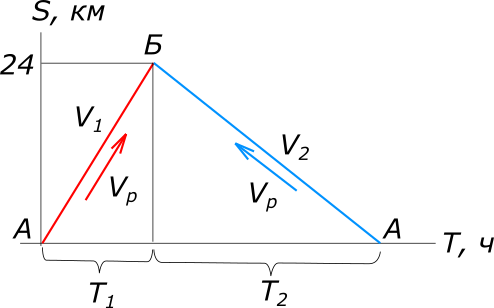
рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{2}-T_{1}=0,5$

$\frac{S}{V_{2}}-\frac{S}{V_{1}}=\frac{1}{2}$

$\frac{S}{V_{к}-V_{р}}-\frac{S}{V_{к}+V_{р}}=\frac{1}{2}$

$V_{к}^2-4SV_{р}-V_{р}^2=0$

$V_{к_{1}}=14; V_{к_{1}}=-14$

Ответ: собственная скорость катера 14 км/ч.