Промедли и ты состаришься остановись и ты умрешь Активность математика Ичиго БанкайЛюбимые темы математика Ичиго БанкайЛучшие решения математика Ичиго БанкайНайти полярные координаты
Вот что нарисовалось на графике 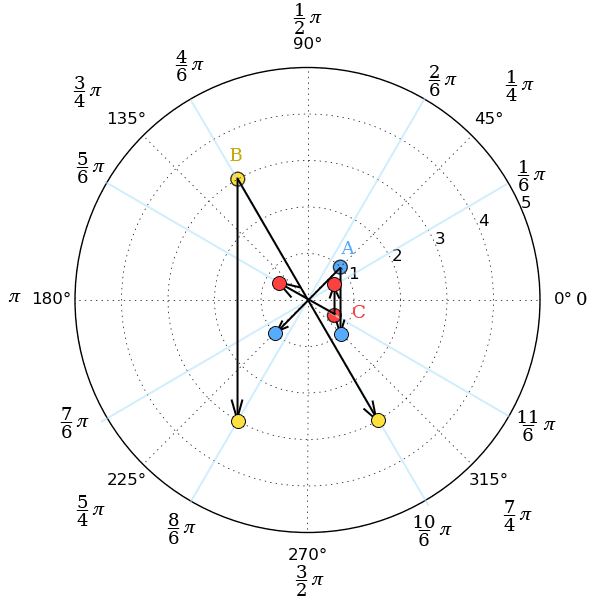
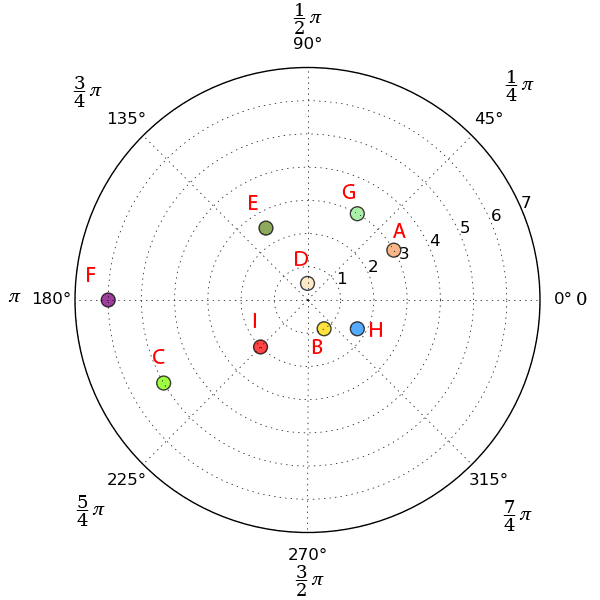
рисунок 1 Для рисования относительно полюса угол преобразуется по следующему правилу (радиус не меняется) формула 1
$ \phi → \phi + \pi $ Для рисования относительно полярной оси угол преобразуется по следующему правилу (радиус не меняется) формула 2
$ \phi → 2\pi - \phi $ Получаем три точки симметричные относительно полюса: формула 3
$ A_{сим.пол} (1; \frac{5}{4} \pi) $ формула 4
$ B_{сим.пол} (3; \frac{5}{3} \pi) $ формула 5
$ C_{сим.пол} (\frac{2}{3}; \frac{5}{6} \pi) $ Получаем три точки симметричные относительно полярной оси: формула 6
$ A_{сим.ос} (1; \frac{7}{4} \pi) $ формула 7
$ B_{сим.ос} (3; \frac{4}{3} \pi) $ формула 8
$ C_{сим.ос} (\frac{2}{3}; \frac{1}{6} \pi) $ КомментарииВ кубе A B C D A1 B1 C1 D1 проведено сечение через середины ребер AB, AD и BB. Каким многоугольником является сечение?
Рисую рисунок 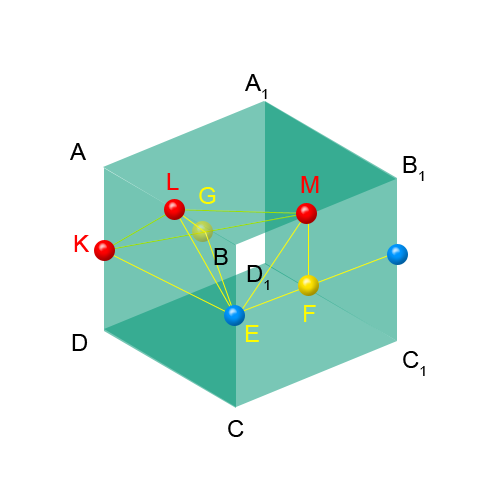
рисунок 1 Нарисовав требуемые середины ребер куба мы видим треугольник из этих точек который принадлежит секущей плоскости KLM. Однако как пойдет плоскость из рисунка не совсем ясно и какие стороны и как она пересечет тоже. Поэтому надо поразмыслить. Я построил дополнительные точки EFG. E - это середина ребра BC. F центр стороны B-B1-C1-C. G середина КМ. При помощи треугольника KEM мы найдем длину KM. и найдем в треугольнике KLM его углы. Потом найдем KG и GM и при помощи них и треугольников KEM найдем стороны и углы LGE. Вот углы это и есть отправная точка к окончательному решению. но пока отложу его на завтра. В общем на меня снизошло озарение - это же куб, он симметричный, и если продолжить построение по законам симметрии то получим все точки пересечения с ребрами куба и соответсвено секущую плоскость - которая получилась правильным шестиугольником 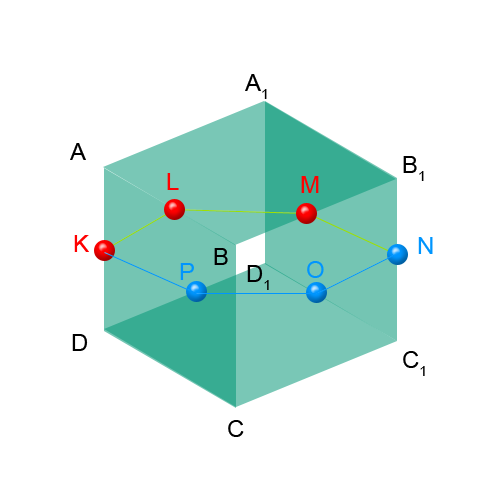
рисунок 2 ответ: секущая плоскость - правильный шестиугольник КомментарииСколько килограммов сливочного масла получил каждый магазин?
Ага. Значит надо составить уравнение для этой задачи. Неизвестную часть сливочного масла обозначим как x. Первый магазин
$ 568 + x $ Второй магазин
$ 624 + x $ Третий магазин
$ 401 + x $ А теперь главное уравнение задачи главное уравнение задачи
$ (568 + x) + (624 + x) + (401 + x) = 3840 $ Раскрываем скобки и упрощаем
$ 3x + 1593 = 3840 $
$ x = \frac{3840 - 1593}{3} = \frac{2247}{3} = 749 $ одинаковая часть - 749 килограммов. Ответ: килограммов сливочного масла получил Первый магазин
$ 568 + 749 = 1317 $ килограммов сливочного масла получил Второй магазин
$ 624 + 749 = 1373 $ килограммов сливочного масла получил Третий магазин
$ 401 + 749 = 1150 $ КомментарииСколько способов перестановки?
Я думаю так: Тома не учитывая то, что третий и четвертый рядом не стоят можно расставить 30! способами. И из этого числа надо вычесть число перестановок когда третий и четвертый стоят рядом. Если рассуждать логически то когда они стоят рядом они могут стоять как 3-4 или как 4-3. В сочетании 3-4 может получится 29 перестановок - т.е. том 3 может стоять с 1 по 29 место. И аналогично 4-3 тоже 29 перестановок - том 4 стоит с 1 по 29 место. итого получиться формула 1
$ 30! - 2*29 = 30! - 58 $ КомментарииСложнейшие задачи математика Ичиго Банкай Тема задачи: Комбинаторика
Сколько красок в палитре у художника? Тема задачи: Комбинаторика
Сколько красок в палитре у художника?
27 августа 2015 22:37
0 подписчиков
1406 просмотров
1
решение |
Записать новую задачу Все задачи Все темы Все математики |








Комментарии