@NICK Обо мне

Создано: @nick 8 августа 2016 12:06

поставьте оценку:

2 голосов, средний бал: 5.0000

Дано: лодка прошла по течению реки и затем возвращается против течения

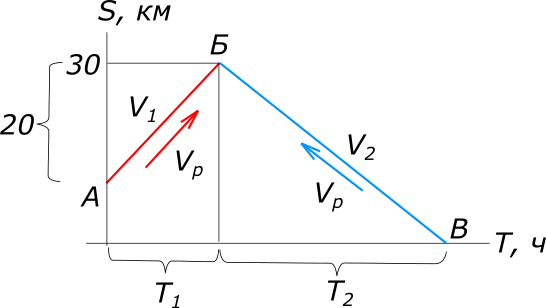
рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{1}+T_{2}=\frac{20}{3}$

$\frac{S_{1}}{V_{1}}+\frac{S_{2}}{V_{2}}=\frac{20}{3}$

$\frac{S_{1}}{V_{л}+V_{р}}+\frac{S_{2}}{V_{л}-V_{р}}=\frac{20}{3}$

$3S_{1}V_{л}-3S_{1}V_{р}+3S_{2}V_{л}+3S_{2}V_{р}=20V_{л}^2-20V_{р}^2$

$20V_{л}^2-3(S_{1}+S_{2})V_{л}-3(S_{2}-S_{1})V_{р}-20V_{р}^2=0$

$V_{л_{1}}=9; V_{л_{1}}=-1,5$

Ответ: собственная скорость лодки 9 км/ч.

Создано: @nick 6 августа 2016 07:49

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: глиссер проплыл по реке и вернулся обратно

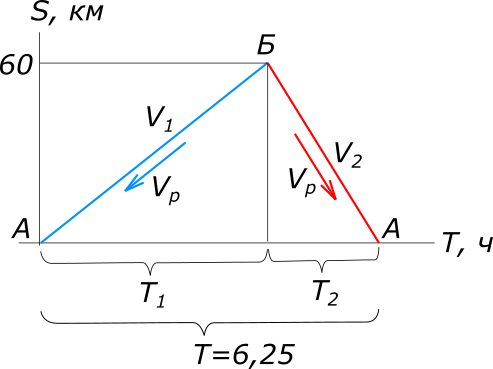
рисунок 1

Изобразим условия задачи на рисунке, выбрав произвольно направление течения реки. Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $T=T_{1}+T_{2}$

$\frac{S}{V_{1}}+\frac{S}{V_{2}}=T$

$\frac{S}{V_{гл}-V_{р}}+\frac{S}{V_{гл}+V_{р}}=T$

$S(V_{гл}+V_{р})+S(V_{гл}-V_{р})=T(V_{гл}-V_{р})(V_{гл}+V_{р})$

$2SV_{гл}=TV_{гл}^2-V_{р}^2$

$V_{р}=sqrt{\frac{TV_{гл}^2-2SV_{гл}}{T}}, откуда V_{р}=4 \frac{км}{ч}$

Ответ: Скорость течения реки равна 4 км/ч

Создано: @nick 23 июля 2016 15:34

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: арифметическая прогрессия

Сумма арифметической прогрессии $S_{n}=\frac{1}{2}(a_{1}+(a_{1}+d(n-1)))n$

Или $S_{1...20}=a_{1}+(a_{1}+d)+(a_{1}+2d)+(a_{1}+3d)+(a_{1}+2d)+...+(a_{1}+19d)$

Для нечетных номеров

Для четных номеров

$S_{2...20}-S_{1...19}=10a_{1}+100d-10a_{1}-90d=10d=80, откуда d$=8

Ответ: разность прогрессии равна 8.

Создано: @nick 24 июля 2016 14:14

поставьте оценку:

1 голосов, средний бал: 5.0000

$51−3n>0, откуда 51>3n и 17>n$

$a_{n}=51−3n, тогда a_{1}=51−3×(1)=48 и a_{2}=51−3×(2)=45, откуда d=a_{2}-a_{1}=-3$

Вычисляем сумму арифметической прогрессии $Sa_{n}=\frac{(a_{1}+a_{n})n}{2}=\frac{(a_{1}+a_{16})16}{2}=\frac{(48+3)16}{2}$=408

Ответ: сумма положительных членов арифметической прогрессии равна 408.

Создано: @nick 24 июля 2016 15:03

поставьте оценку:

1 голосов, средний бал: 5.0000

Определим максимальное число отрицательных членов $a_{n}=5n-100, откуда 0>5n-100, тогда 100>5n, и 20>n, принимаем n=19$

Определим разность прогрессии $a_{1}=5×1-100=-95, a_{2}=5×2-100=-90, d=a_{2}-a_{1}=-90-(-95)=5$

Вычисляем сумму $S=\frac{(a_{1}+a_{n})n}{2}=\frac{(-95-5)19}{2}$=950

Ответ: сумма всех отрицательных членов данной арифметической прогрессии равна -950.