@NICK @nick

@NICK Решения
28 Прислал задач
31 Написал решений
5.0000 Средний балл за решения
Обо мне Задачи Решения Подписки На задачи На темы На математиков

Все решения математика @NICK

Решить задание ЕГЭ
Создано: @nick 14 декабря 2024 11:19
поставьте оценку:
0 голосов, средний бал: 0.0000

Пример текста

Решить задание ЕГЭ
Создано: @nick 8 июля 2019 11:33
поставьте оценку:
0 голосов, средний бал: 0.0000

Решить задание ЕГЭ

Перепишем данное выражение

$ \frac{(728^{2} - 26^{2})} {756} $

Выполним преобразования

$ \frac{(728 - 26)(728 + 26)}{(728 + 26)} $

После сокращения подобных членов получим

$ \frac{(728 - 26)1}{1}=728-26=702 $

Ответ: 702.

Решить задание ЕГЭ
Создано: @nick 7 июля 2019 21:05
поставьте оценку:
0 голосов, средний бал: 0.0000

Решить задание ЕГЭ Уравнение представлено в виде равенства двух дробей. Их числители одинаковы, а это значит, что их знаменатели равны между собой.

$ 5x+7 = 7x+5 $

приводим подобные члены уравнения

$ 7x - 5x = 7 - 5 $

Или

$ 2x = 2 $

Откуда

$ x = 1 $

Знаменатели дробей не могут быть равны нулю

$ 5x+7 ≠ 0 ∧ 7x+5 ≠ 0 $

Дроби, также, равны когда их числители равны нулю

$ x + 8 = 0 $

Откуда находим еще один корень уравнения

$ x = - 8 $

Ответ: x=1.

Решить задание ЕГЭ
Создано: @nick 7 июля 2019 18:19
поставьте оценку:
0 голосов, средний бал: 0.0000

Решить задание ЕГЭ Записываем, что дано по условию задачи

таблица 1

Начальная сумма денег у Маши$S_{нач}$$350$$₽$
Стоимость покупки$S_{пок}$
Цена  орехов$υ$$75$$\frac{₽}{кг}$
Вес орехов$t$$4,4$$кг$
Конечная сумма денег у Маши$S_{к}$$?$$₽$

Составляем уравнение, основываясь на записанных в таблицу данных задачи

$ S_{нач}=S_{пок}+S_{к} $

Где

$ S_{пок}=υt $

Тогда

$ S_{к} = S_{нач}-S_{пок}=S_{нач}-υt=350-75×4,4=350-330=20 ₽ $

Маша должна получить 20 ₽ сдачи.

Сколько кирпичей уйдет на каждую стену?
Создано: @nick 16 августа 2016 20:40
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: две кирпичные стены, которые выкладывает каменщик

$S_{1}$ - количество кирпичей в первой стене$шт$
$S_{2}$ - количество кирпичей во второй стене
$S_{1}-S_{2}$2000$шт$
$S$ - количество кирпичей в первой и второй стене6200$шт$
$S_{1}-? и S_{1}-?$

Решение:

$S=S_{1}+S_{2}= 6200$
$S_{1} = 2000 + S_{2}$
$2000+S_{2}+S_{2}= 6200$
$S_{2}= \frac{6200-2000}{2}=2100$
$S_{1} = 2000 + S_{2}=2000+2100=4100$

Ответ: количество кирпичей в первой и второй стене 4100 и 2100 соответственно.

Через сколько времени велосипедист догонит бегуна?
Создано: @nick 16 августа 2016 18:19
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: велосипедист догоняет бегуна

$T_{б}$ - время в пути бегуна
$T_{в}$ - время в пути велосипедиста
$T_{б}-T_{в}$$\frac{1}{3}$$ч$
$S_{x}$ - расстояние до места встречи
$V_{б}$16$\frac{км}{ч}$
$V_{в}-V_{б}$5$\frac{км}{ч}$
$T_{в}$-?

Изобразим условия задачи на рисунке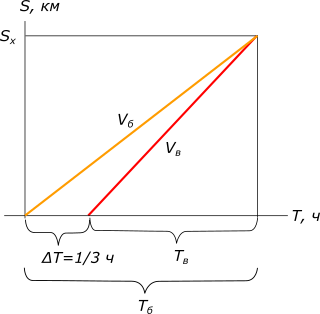

рисунок 1

рисунок 1

Решение:

$S=VT$  - уравнение равномерного прямолинейного движения
$S_{б}=S_{в}$
$V_{б}T_{б}=V_{в}T_{в}, учитывая что T_{б}=T_{в}+\frac{1}{3}=\frac{3Tв+1}{3}$
$V_{б}(3T_{в}+1)=3V_{в}T_{в}$
$V_{б}=(3V_{в}-3V_{б})T_{в}$
$T_{в}=\frac{V_{б}}{3(Vв-Vб)}=1,067$

Ответ: велосипедист догонит бегуна через 1,067 ч

С какой скоростью ехал мотоциклист
Создано: @nick 16 августа 2016 14:28
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: велосипедист и мотоциклист проехали из пункта А в пункт Б

$S$ - расстояние между городами120$км$
$T_{в}$ - время в пути велосипедиста
$T_{м}$ - время в пути мотоциклиста
$T_{в} - T{м}$6$ч$
$V_{м}$ - скорость мотоциклиста
$V_{в}$ - скорость велосипедиста
$V_{м}-V_{в}$10$\frac{км}{ч}$
$V_{м}$ - ?

Изобразим условия задачи на рисунке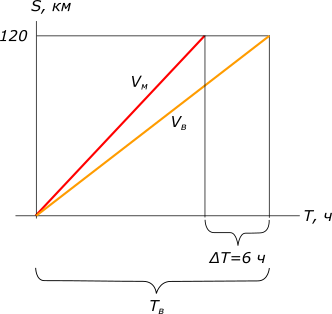

рисунок 1

рисунок 1

Уравнение равномерного прямолинейного движения $S=VT, откуда T=\frac{S}{V}$

По условиям задачи составляем уравнение:

$\frac{S}{V_{в}}-\frac{S}{V_{м}}=6$
$\frac{S}{V_{м}-10}-\frac{S}{V_{м}}=6$
$SV_{м}-S(V_{м}-10)=6(V_{м}-10)V_{м}$
$10S=6V_{м}V_{м}-60V_{м}$
$3V_{м}V_{м}-30V_{м}-1000=0$
$V_{м_{1}}=23,93 и V_{м_{1}}=-13,93$

Ответ: скорость мотоциклиста 23,93 км/ч

Сколько страниц в час печатает каждая машинистка?
Создано: @nick 15 августа 2016 19:14
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: две машинистки перепечатывают рукопись порозь и вместе

$S$ - объем рукописи200$стр$
$S_{1_{1}}$ - объем  рукописи перепечатанный 1-ой машинисткой  порозьS25%
$S_{2_{1}}$ - объем  рукописи перепечатанный 2-ой машинисткой  порозь20$стр$
$T_{одн}$ - время одновременной работы  машинисток
$T_{1}$ - время работы 1-ой машинистки в одиночку
$T_{2}$ - время работы 1-ой машинистки в одиночку
$V_{1}$ - скорость работы 1-ой машинистки
$V_{2}$ - скорость работы 2-ой машинистки
$T$ - время перепечатывания машинистками всей рукописи6 ч 40 мин$\frac{20}{3}ч$
$V_{1}+V_{2}$44$\frac{стр}{ч}$
$V_{2} < V_{1}$
$V_{1}=? и V_{2}=?$

Изобразим условия задачи на рисунке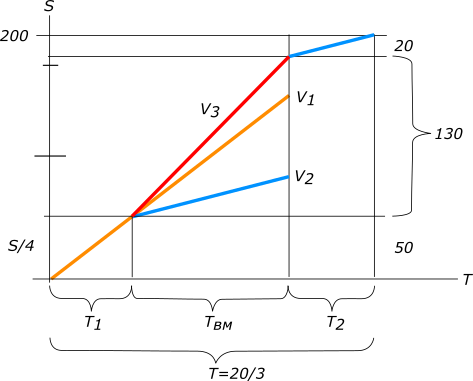

рисунок 1

рисунок 1

$V_{1}+V_{2}=44, откуда V_{2}=44-V_{1}$

Когда машинистки работают одновременно

$T_{одн}=\frac{S_{одн}}{V_{1}+V_{2}}=\frac{130}{44}$

Когда машинистки работают порозь

$T=T_{1}+T_{2}$
$T=\frac{S_{1_{1}}}{V_{1}}+\frac{S_{2_{1}}}{V_{2}}$
$T=\frac{50}{V_{1}}+\frac{20}{V_{2}}=\frac{20}{3}-\frac{130}{44}$
$50V_{2}+20V_{1}=(\frac{20}{3}-\frac{130}{44})V_{1}V_{2}$
$132×50V_{2}+132×20V_{1}=(880-390)V_{1}V_{2}$
$132×5V_{2}+132×2V_{1}=49V_{1}V_{2}$
$132×5(44-V_{1})+264V_{1}=49V_{1}(44-V_{1})$
$29040-660V_{1}+264V_{1}=2156V_{1}-49V_{1}V_{1}$
$49V_{1}V_{1}-2552V_{1}+29040=0$
$V_{1_{1}}=35,286 и V_{1_{2}}=16,796$

Согласно условию задачи принимаем $V_{1}=35,286 , тогда V_{2}=44-35,286=8,714$

Ответ: 35,286 страниц в час печатает первая машинистка и 8,714 страниц в час печатает вторая машинистка.

Какой объем грунта каждый экскаватор выбирает за 1 час?
Создано: @nick 11 августа 2016 14:15
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: два экскаватора выкапывают котлован сначала первую половину затем вторую

$S$ - объем котлована2000$м^3$
$S_{1_1}$ - объем грунта, выбранный 1-ым экскаватором на 1-ой половине котлованаS20%
$S_{2_1}$ - объем грунта, выбранный 2-ым экскаватором на 1-ой половине котлованаS30%
$T_{2п}$ - время работы экскаваторов на 2-ой половине котлована
$T_{1п}=T_{2п}+25$ - время работы экскаваторов на 1-ой половине котлована
$V_{1}$ - производительность работы 1-ого экскаватора
$V_{2}$ - производительность работы 2-ого экскаватора
$V_{1}+V_{2}$100$\frac{м^3}{ч}$
 $V_{2} < V_{1}$
$V_{1}=? и V_{2}=?$
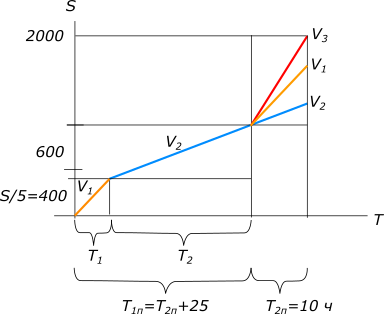
рисунок 1

рисунок 1

2-я половина котлована

${V_{1}+V_{2}=100 , откуда V_{1}=100-V_{2}$
$T_{2п}=\frac{\frac{1}{2}S}{V_{1}+V_{2}}=\frac{1000}{100}=10$

1-я половина котлована

$T_{1п}=T_{2п}+25=35$
$T_{1п}=\frac{S_{1_{1}}}{V_{1}}+\frac{S_{2_{1}}}{V_{2}}=35$
$400V_{2}+600V_{1}=35V_{1}V_{2}$
$8000-80V_{1})+120V_{1}=700V_{1}-7V_{1}V_{1}$
$7V_{1}V_{1}-660V_{1}+8000=0$
$V_{1_{1}}=80 b V_{1_{2}}=14,286$

Согласно условию выбраем $V_{1}=80, тогда V_{2}=100-V_{1}=20$

Ответ: первый экскаватор за 1 час выбирает объем грунта равный 80 м.куб., 2-ой - 20 м. куб.

Сколько килограммов олова содержится в новом сплаве?
Создано: @nick 10 августа 2016 18:34
поставьте оценку:
0 голосов, средний бал: 0.0000
Лучшее Решение

Дано: два сплава состоящие из меди, цинка и олова

$спл_{1}$$спл_{2}$
$p_{0_{1}}=40%$$p_{м_{2}}=26%$
$p_{ц_{1}}=p_{ц_{2}}$$p_{ц_{2}}=p_{ц_{1}}$
$m_{1}=150 кг$$m_{2}=250 кг$

Сплавив сплав_1 и сплав_2 получили новый сплав_3

$m_{3}=m_{1}+m_{2}=150+250=400 кг$
$p_{ц_{3}}=30%$
$p_{о_{3}}-?$
Решение:
$m_{о_{1}}=m_{1}p_{о_{3}}=150×0,4=60 кг$
$m_{м_{2}}=m_{2}p_{м_{2}}=250×0,26=65 кг$
$m_{ц_{3}}=m_{3}p_{ц_{3}}=400×0,3=120 кг$
$m_{ц_{3}}=m_{1}p_{ц_{1}}+m_{2}p_{ц_{2}}=(m_{1}+m_{2})p_{ц_{1}}$
$p_{ц_{1}}=\frac{m_{ц_{3}}}{m_{1}+m_{2}}=\frac{120}{150+250}=30%$
$m_{ц_{1}}=m_{1}p_{ц_{1}}=150×0,3=45 кг$
$m_{ц_{2}}=m_{2}p_{ц_{2}}=250×0,3=75 кг$
$m_{м_{1}}=m_{1}-m_{о_{1}}-m_{ц_{1}}=150-60-45=45 кг$
$m_{о_{2}}=m_{2}-m_{м_{2}}-m_{ц_{2}}=250-65-75=110 кг$
$m_{о_{3}}=m_{о_{1}}+m_{о_{2}}=60+110=170 кг$ 

Ответ: в новом сплаве содержится 170 кг олова.

Сколько килограммов меди содержится в новом сплаве?
Создано: @nick 10 августа 2016 15:46
поставьте оценку:
0 голосов, средний бал: 0.0000
Лучшее Решение

Дано: два сплава состоящие из меди, цинка и олова

$спл_{1}$$спл_{2}$
$p_{ц_{1}}=25%$$p_{м_{2}}=50%$
$p_{о_{1}}=2p_{о_{2}}$$p_{о_{2}}$
$m_{1}=200 кг$$m_{2}=300 кг$

Сплавив сплав_1 и сплав_2 получили новый сплав_3

$спл_{3}$
$p_{ц_{3}}=28%$
$m_{м_{3}}$ - ?

Решение:

$m_{м_{2}}=m_{2}p_{м_{2}=300×0,5$ = 150 кг
$m_{ц_{1}}=m_{1}p_{ц_{1}}=200×0,25$ = 50 кг
$m_{ц_{3}}=m_{3}p_{ц_{3}}=500×0,28$ = 140 кг
$m_{ц_{3}}=m_{ц_1}+m_{ц_{2}}=40+m_{ц_{2}}=140 кг; m_{ц_{2}}$=  100 кг
$m_{о_{2}}=m_{2}-m_{м_{2}}-m_{ц_{2}}=300-150-100$ = 50 кг
$p_{о_{2}}=\frac{m_{о_{2}}}{m_{2}}100%=\frac{50}{300}100%$ = 16,67%
$p_{о_{1}}=2p_{о_{2}}=2×16,67%$ = 33,34%
$m_{о_{1}}=m_{1}p_{о_{1}}=200×0,3334$ = 66,68 кг
$m_{м_{1}}=m_{1}-m_{ц_{1}}-m_{о_{1}}=200-50-66,68$ = 83,32 кг
$m_{м_{3}}=m_{м_{1}}+m_{м_{2}}=83,32+150$ = 233,32 кг

Ответ: в получившемся новом сплаве содержится 233,32 кг меди.

Какой пробы было золото
Создано: @nick 10 августа 2016 08:46
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: две пары золотых слитков

$спл_{1}$$спл_{2}$$спл_{3}$$спл_{4}$
$m_{1}=40 г$$m_{2}=60 г$$m_{3}=m$$m_{4}=m$
$p_{1}=?$$p_{2}=?$$p_{3}=p_{1}$$p_{4}=p_{2}$

получены сплавы золотых слитков 1, 2 и 3, 4

$спл_{1,2}$$спл_{3,4}$
$m_{1,2}=100 г$$m_{3,4}=2m$
$p_{1,2}=62%$$p_{3,4}=61%$
Решение:Решение:
$m_{1}p_{1}+m_{2}p_{2}=m_{1,2}p_{1,2}$$m_{3}p_{1}+m_{4}p_{2}=m_{3,4}p_{3,4}$
$m(p_{1}+p_{2})=2m×0,61$
$p_{2}=2×0,61-p_{1}$
$40p_{1}+60(2×0,61-p_{1})=100×0,62$
$p_{1}=\frac{73,2-62}{20}$ = 0,56
$p_{2}=2×0,61-0,56$ = 0,66

Ответ: пробы золота 1-ого и 2-ого слитков 56% и 66% соответственно.

Найти скорость первого лыжника
Создано: @nick 8 августа 2016 18:51
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: лыжник догоняющий на трассе сначала одного а затем второго соперника

$S_{1}$Путь который проходит второй лыжник
$S_{2}$Путь который проходит первый лыжник
$S_{3_{1}} и S_{3_{2}}$Путь который проходит третий лыжник
$V_{1}=\frac{7}{6}V_{2}$Скорость первого лыжника
$V_{2}$Скорость второго лыжника
$V_{3}$Скорость третьего лыжника18$\frac{км}{ч}$
$T_{с_{1}}=T_{с_{2}}$Время старта первого и второго лыжника0
$T_{с_{3}}$Время старта третьего лыжника$\frac{1}{3}ч$
$T$Время обгона первого лыжника$ч$
$T_{1}=T$Время в пути первого лыжника$ч$
$T_{2}=T-\frac{1}{2}$Время в пути второго лыжника$ч$
$T_{3_{1}}=T-\frac{1}{2}-\frac{1}{3}$Время в пути третьего лыжника первый обгон$ч$
$T_{3_{2}}=T-\frac{1}{2}$Время в пути третьего лыжника второй обгон$ч$
$V_{1}$?
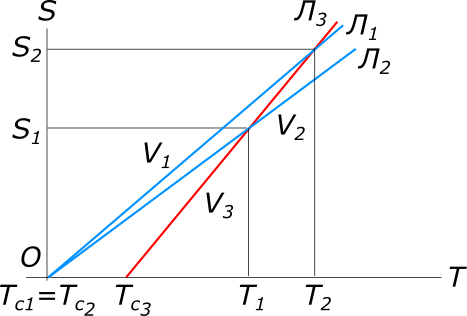
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнения:

обгон второго лыжникаобгон первого лыжника 
$S_{1}=S_{3_{1}}$$S_{2}=S_{3_{2}}$
$V_{2}T_{1}=V_{3}(T_{1}-T_{с_{3}})$$V_{1}T=V_{3}(T-T_{с_3})$
$V_{2}(T-\frac{1}{2})=V_{3}((T-\frac{1}{2})-\frac{1}{3})$$V_{1}T=V_{3}(T-\frac{1}{3})$
$T=\frac{\frac{5}{6}V_{3}-\frac{1}{2}V_{2}}{V_{3}-V_{2}}$$T=\frac{\frac{1}{3}V_{3}}{V_{3}-V_{1}}$

$V_{1}=\frac{7}{6}V_{2}, откуда V_{2}=\frac{6}{7}V_{1}$

Тогда $\frac{\frac{5}{6}V_{3}-\frac{1}{2}\frac{6}{7}V_{1}}{V_{3}-\frac{6}{7}V_{1}}=\frac{\frac{1}{3}V_{3}}{V_{3}-V_{1}}$

$(\frac{5}{6}V_{3}-\frac{1}{2}\frac{6}{7}V_{1})(V_{3}-V_{1})=\frac{1}{3}V_{3}(V_{3}-\frac{6}{7}V_{1})}$

$\frac{5}{6}V_{3}^2-\frac{3}{7}V_{1}V_{3}-\frac{5}{6}V_{3}V_{1}+\frac{3}{7}V_{1}^2=\frac{1}{3}V_{3}^2-\frac{2}{7}V_{3}V_{1}$

$18V_{1}^2-41V_{1}V_{3}+21V_{3}^2=0$

$V_{1_{1}}=27; V_{1_{2}}=14$

Ответ: скорость первого лыжника 14 км/ч.

Найти собственную скорость лодки
Создано: @nick 8 августа 2016 12:06
поставьте оценку:
2 голосов, средний бал: 5.0000
Лучшее Решение

Дано: лодка прошла по течению реки и затем возвращается против течения

$S_{1}$ - путь пройденный лодкой по течению реки20$км$
$S_{2}$ - путь пройденный лодкой против течения 30$км$
$V_{1}$ - скорость лодки по течению
$V_{2}$ - скорость лодки против течения
$T_{1}$ - время лодки в пути по течению
$T_{2}$ - время лодки в пути против течения
$T_{1}+T_{2}=T$$6 ч 40 мин$$\frac{20}{3}ч$
$V_{р}$ - скорость реки3$\frac{км}{ч}$
$V_{к}$ - скорость катера в стоячей воде?
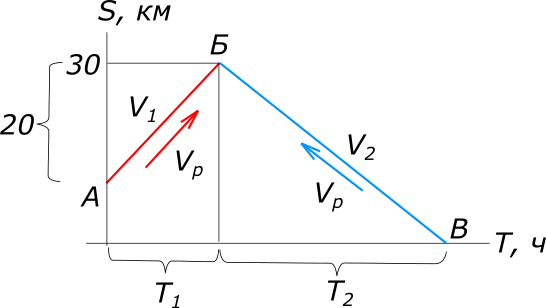
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{1}+T_{2}=\frac{20}{3}$

$\frac{S_{1}}{V_{1}}+\frac{S_{2}}{V_{2}}=\frac{20}{3}$

$\frac{S_{1}}{V_{л}+V_{р}}+\frac{S_{2}}{V_{л}-V_{р}}=\frac{20}{3}$

$3S_{1}V_{л}-3S_{1}V_{р}+3S_{2}V_{л}+3S_{2}V_{р}=20V_{л}^2-20V_{р}^2$

$20V_{л}^2-3(S_{1}+S_{2})V_{л}-3(S_{2}-S_{1})V_{р}-20V_{р}^2=0$

$V_{л_{1}}=9; V_{л_{1}}=-1,5$

Ответ: собственная скорость лодки 9 км/ч.

Найти собственную скорость катера
Создано: @nick 8 августа 2016 10:08
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: катер плывет по течению реки вниз и затем возвращается против течения

$S$ - путь пройденный катером по течению и против течения24$км$
$V_{1}$ - скорость катера по течению$\frac{км}{ч}$
$V_{2}$ - скорость катера против течения$\frac{км}{ч}$
$T_{1}$ - время катера в пути по течению
$T_{2}$ - время катера в пути против течения
$T_{2}-T_{1}$0,5$ч$
$V_{р}$ - скорость реки2$\frac{км}{ч}$
$V_{к}$ - скорость катера в стоячей воде?
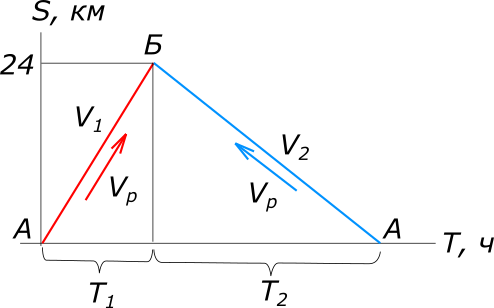
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{2}-T_{1}=0,5$

$\frac{S}{V_{2}}-\frac{S}{V_{1}}=\frac{1}{2}$

$\frac{S}{V_{к}-V_{р}}-\frac{S}{V_{к}+V_{р}}=\frac{1}{2}$

$V_{к}^2-4SV_{р}-V_{р}^2=0$

$V_{к_{1}}=14; V_{к_{1}}=-14$

Ответ: собственная скорость катера 14 км/ч.

Найти скорость яхты в стоячей воде
Создано: @nick 7 августа 2016 15:57
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: яхта плывет по течению и затем возвращается против течения

$S$ - путь пройденный яхтой по течению и против течения9$км$
$V_{1}$ - скорость яхты по течению$\frac{км}{ч}$
$V_{2}$ - скорость яхты против течения$\frac{км}{ч}$
$T_{1}$ - время яхты в пути по течению
$T_{2}$ - время яхты в пути против течения
$V_{р}$ - скорость реки3$\frac{км}{ч}$
$V_{я}$ - скорость яхты в стоячей воде?
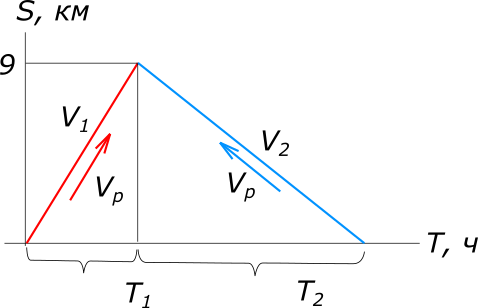
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{2}-T_{1}=2$

$\frac{S}{V_{2}}-\frac{S}{V_{1}}=2$

$\frac{S}{V_{я}-V_{р}}-\frac{S}{V_{я}+V_{р}}=2$

$2V_{я}^2-2SV_{р}-2V_{р}^2=0$

$V_{я_{1}}=6; V_{я_{1}}=-6$

Ответ: скорость яхты в стоячей воде 6 км/ч.

Найти начальную скорость автомобиля
Создано: @nick 7 августа 2016 12:11
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: автомобиль наверставший время в пути

$S$ - Путь который должен пройти автомобиль60$км$
$V_{1}$ - Скорость автомобиля плановая
$∆V$ - Увеличение скорости автомобиля15$\frac{км}{ч}$
$T_{пл}$ - Время в пути по плану
$T_{з}$ - Задержка в пути0,2$ч$
$V_{2}$ - Скорость автомобиля увеличенная
$V_{1}$?
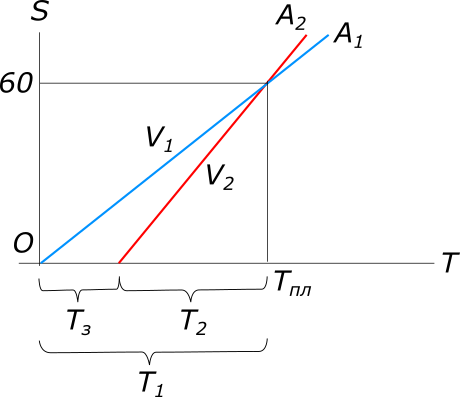
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $\frac{S}{V_{1}}-\frac{S}{V_{2}}=0,2$

Но $V_{2}=V_{1}+15, тогда \frac{S}{V_{1}}-\frac{S}{V_{1}+15}=0,2$

$S(V_{1}+15)-SV_{1}=0,2V_{1}(V_{1}+15)$

$0,2V_{1}^2+3V_{1}-15S=0$

$V_{1_{1}}=60; V_{1_{2}}=-75$

Ответ: начальная скорость автомобиля составляла 60 км/ч.

Определить время в которое баржа приплыла в пункт Б
Создано: @nick 7 августа 2016 09:04
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: баржа плывущая вверх и вниз по реке с остановкой

$T_{отпр_{А}}$ - время отправления из пункта А9$ч$
$S_{1}$ - расстояние пройденное против течению60$км$
$S_{2}$ - расстояние пройденное по течению60$км$
$T_{1}$ - время в пути вверх по реке$ч$
$T_{с}$ - время стоянки в пункте Б$ч$
$T_{2}$ - время в пути вниз по реке$ч$
$V_{б}$ - скорость баржи в стоячей воде$\frac{км}{ч}$
$V_{р}$ - скорость реки3$\frac{км}{ч}$
$T_{приб_{А}}$ - время прибытия в пункт А19 ч 20 мин$19,33 ч$
$T_{приб_{Б}}$ - время прибытия в пункт Б?$ч$

Изобразим условия задачи на рисунке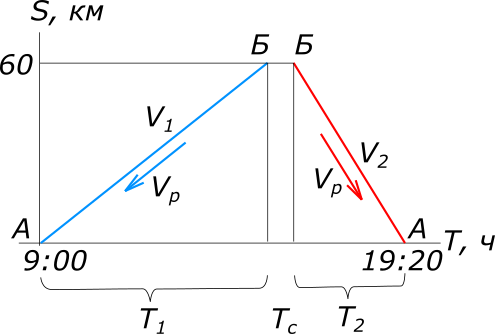

рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $T_{приб_{А}}=T_{отпр_{А}}+T_{1}+T_{2}+T_{с}$

$\frac{S_{1}}{V_{1}}+\frac{S_{2}}{V_{2}}=T_{приб_{А}}-T_{отпр_{А}}-T_{с}$

$\frac{S_{1}}{V_{б}-V_{р}}+\frac{S_{2}}{V_{б}+V_{р}}=8,33$

$S_{1}(V_{б}+V_{р})+S_{2}(V_{б}-V_{р})=8,33(V_{б}-V_{р})(V_{б}+V_{р}), но S_{1}=S_{2}=S$

$8,33V_{б}^2-2SV_{б}-8,33V_{р}^2=0$

Откуда $V_{б_{1}}=15; V_{б_{1}}=0,6 принимаем V_{б}=15$

Составляем уравнение $T_{приб_{Б}}=T_{отпр_{А}}+T_{1}=T_{отпр_{А}}+\frac{S}{V_{б}-V_{р}}=9+\frac{60}{15-3}=14$

Ответ: время прибытия баржи в пункт Б 14 ч.

Определить скорость течения реки
Создано: @nick 6 августа 2016 15:46
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: моторная лодка прошела по течению реки и затем против

$S_{1}$ - расстояние пройденное по течению25$км$
$S_{2}$ - расстояние пройденное против течения3$км$
$T$ - время на весь путь2$ч$
$V_{л}$ - скорость лодки в стоячей воде12$\frac{км}{ч}$
$V_{р}$ - скорость реки?
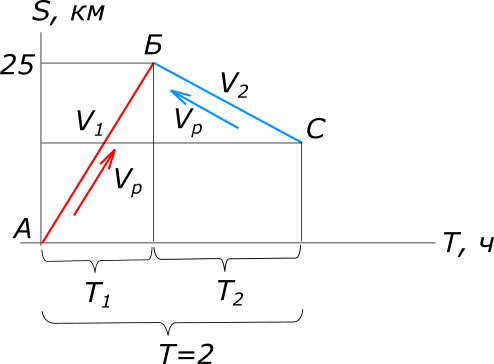
рисунок 1

рисунок 1

Изобразим условия задачи на рисунке. Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $T=T_{1}+T_{2}$

$\frac{S_{1}}{V_{1}}+\frac{S_{2}}{V_{2}}=T$

$\frac{S_{1}}{V_{л}+V_{р}}+\frac{S_{2}}{V_{л}-V_{р}}=T$

$25(V_{л}-V_{р})+3(V_{л}+V_{р})=2(V_{л}+V_{р})(V_{л}-V_{р})$

$2V_{р}^2-22V_{р}-2V_{л}^2+28V_{л}=0$

откуда $V_{р_{1}}=8; V_{р_{2}}=3$

Ответ: скорость течения реки равна 3 км/ч.

Определить собственную скорость теплохода
Создано: @nick 6 августа 2016 13:11
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: теплоход прошел по реке и вернулся обратно

$S$ - расстояние туда и обратно48$км$
$T$ - время на весь путь5$ч$
$V_{р}$ - скорость течения реки4$\frac{км}{ч}$
$V_{т}$ - собственная скорость теплохода?
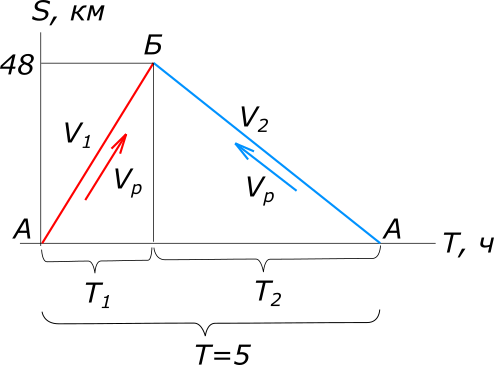
рисунок 1

рисунок 1

Изобразим условия задачи на рисунке. Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $T=T_{1}+T_{2}$

$\frac{S}{V_{1}}+\frac{S}{V_{2}}=T$

$\frac{S}{V_{т}+V_{р}}+\frac{S}{V_{т}-V_{р}}=T$

$S(V_{т}-V_{р})+S(V_{т}+V_{р})=T(V_{т}+V_{р})(V_{т}-V_{р})$

$TV_{т}^2-2SV_{т}-TV_{р}^2=0$

откуда $V_{т_{1}}=20; V_{т_{2}}=-0,8$

Ответ: собственная скорость теплохода равна 20 км/ч.

Определить скорость течения реки
Создано: @nick 6 августа 2016 07:49
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано: глиссер проплыл по реке и вернулся обратно

$V_{гл}$-собственная скорость глиссера20$\frac{км}{ч}$
$S$-расстояние туда и обратно60км
$T$- время на весь путь6,25ч
$V_{р}$-скорость течения реки?
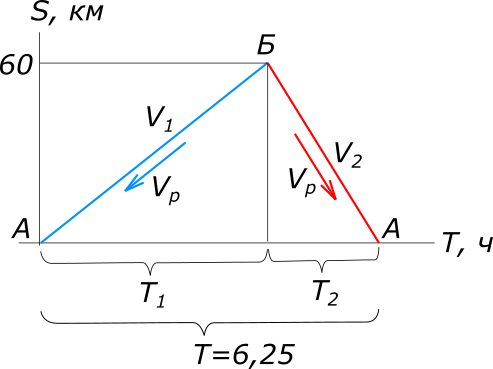
рисунок 1

рисунок 1

Изобразим условия задачи на рисунке, выбрав произвольно направление течения реки. Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

Составляем уравнение: $T=T_{1}+T_{2}$

$\frac{S}{V_{1}}+\frac{S}{V_{2}}=T$

$\frac{S}{V_{гл}-V_{р}}+\frac{S}{V_{гл}+V_{р}}=T$

$S(V_{гл}+V_{р})+S(V_{гл}-V_{р})=T(V_{гл}-V_{р})(V_{гл}+V_{р})$

$2SV_{гл}=TV_{гл}^2-V_{р}^2$

$V_{р}=sqrt{\frac{TV_{гл}^2-2SV_{гл}}{T}}, откуда V_{р}=4 \frac{км}{ч}$

Ответ: Скорость течения реки равна 4 км/ч

С какой скоростью шел пешеход?
Создано: @nick 5 августа 2016 12:21
поставьте оценку:
1 голосов, средний бал: 5.0000
Лучшее Решение

Дано:

$S$Путь который должен пройти пешеход12 км
$V_{1}$Скорость пешехода плановая
$∆V$Увеличение скорости пешехода1$\frac{км}{ч}$
$T_{пл}$Время в пути по плану
$T_{вых_{1}}$Время выхода плановое
$T_{вых_{2}}$Время выхода с задержкой
$∆T$Задержка выхода1ч
$V_{2}$Скорость пешехода увеличенная
$V_{1}$=?
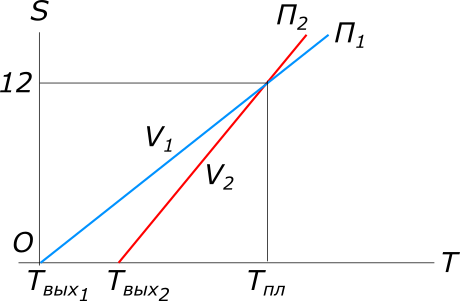
рисунок 1

рисунок 1

Равномерное прямолинейное движение описывается уравнением: $S=VT, откуда T=\frac{S}{V}$

По имеющимся данным задачи составляем уравнение: $T_{пути_{1}}-T_{пути_{2}}=\frac{S}{V_{1}}-\frac{S}{V_{2}}=1$

$V_{2}=V_{1}+1$

$\frac{S}{V_{1}}-\frac{S}{V_{1}+1}$=1

$SV_{1}+S-SV_{1}=V_{1}(V_{1}+1)$

$V_{1}^2+V_{1}-12=0, решая данное квадратное уравнение находим V_{1_{1}}=3 и V_{1_{2}}=-4$

Ответ: пешеход шел со скоростью 3 км/ч.

Найти скорость легкового автомобиля
Создано: @nick 25 июля 2016 15:18
поставьте оценку:
0 голосов, средний бал: 0.0000

Путь грузовика и мотоциклиста до встречи одинаков $S_{гр}=S_{мот}$

$v_{гр}T=v_{мот}(T-0,5)=v_{мот}T-v_{мот}0,5$

$T=\frac{0,5v_{мот}}{v_{мот}-v_{гр}}$

Путь грузовика и автомобиля до встречи одинаков $S_{л. а}=S_{мот}$

$v_{л. а}(T+1)=v_{мот}(T+1-0,5)=v_{мот}(T+1)-0,5v_{мот}$

$0,5v_{мот}=(v_{мот}-v_{л. а})(T+1)$

Тогда $0,5v_{мот}=(v_{мот}-v_{л. а})(\frac{0,5v_{мот}}{v_{мот}-v_{гр}}+1)$

$(\frac{v_{мот}}{v_{мот}-v_{л. а}}-\frac{v_{мот}}{v_{мот}-v_{гр}})=2$

$v_{мот}(v_{мот}-v_{гр})-v_{мот}(v_{мот}-v_{л. а})=2(v_{мот}-v_{л. а})(v_{мот}-v_{гр})$

$v_{мот}((v_{мот}-v_{гр})-(v_{мот}-v_{л. а}))=2(v_{мот}-v_{л. а})(v_{мот}-v_{гр})$

$v_{мот}(v_{л. а}-v_{гр})=2(v_{мот}-v_{л. а})(v_{мот}-v_{гр})$

$v_{мот}\frac{v_{гр}}{5}=2(v_{мот}-v_{л. а})(v_{мот}-v_{гр})$

$v_{мот}v_{гр}=10(v_{мот}-v_{л. а})(v_{мот}-v_{гр})$

$v_{мот}v_{гр}=10(v_{мот}^2-v_{мот}v_{л. а}-v_{мот}v_{гр}+v_{л. а}v_{гр})$

$0=10v_{мот}^2-10v_{мот}\frac{6}{5}v_{гр}-11v_{мот}v_{гр}+10\frac{6}{5}v_{гр}v_{гр}$

$12v_{гр}^2-23v_{мот}v_{гр}+10v_{мот}^2=0$

Решая квадратное уравнение находим: $v_{гр}_{1}=112,5 и v_{гр}_{2}=60, тогда v_{л. а}=\frac{6}{5}v_{гр}=\frac{6}{5}60}=72\frac{км}{ч}$

Ответ: скорость легкового автомобиля составляет 72 км/ч.

Найти скорость легкового автомобиля
Создано: @nick 25 июля 2016 14:58
поставьте оценку:
0 голосов, средний бал: 0.0000

Дано:

$v_{гр}$
$v_{л. а}=\frac{6}{5}v_{гр}$
$v_{мот}$90 км/ч
Время грузовика до встречи мотоциклиста$T$
Время легкового автомобиля до встречи мотоциклиста$T+1$
Время мотоциклиста до встречи грузовика $T-0,5$
Время мотоциклиста до встречи легкового автомобиля$T+1-0,5$
$v_{л. а}$?
Найти сумму всех отрицательных членов арифметической прогрессии
Создано: @nick 24 июля 2016 15:03
поставьте оценку:
1 голосов, средний бал: 5.0000

Определим максимальное число отрицательных членов $a_{n}=5n-100, откуда 0>5n-100, тогда 100>5n, и 20>n, принимаем n=19$

Определим разность прогрессии $a_{1}=5×1-100=-95, a_{2}=5×2-100=-90, d=a_{2}-a_{1}=-90-(-95)=5$

Вычисляем сумму $S=\frac{(a_{1}+a_{n})n}{2}=\frac{(-95-5)19}{2}$=950

Ответ: сумма всех отрицательных членов данной арифметической прогрессии равна -950.

Найдите сумму всех положительных членов прогрессии
Создано: @nick 24 июля 2016 14:14
поставьте оценку:
1 голосов, средний бал: 5.0000

$51−3n>0, откуда 51>3n и 17>n$

$a_{n}=51−3n, тогда a_{1}=51−3×(1)=48 и a_{2}=51−3×(2)=45, откуда d=a_{2}-a_{1}=-3$

Вычисляем сумму арифметической прогрессии $Sa_{n}=\frac{(a_{1}+a_{n})n}{2}=\frac{(a_{1}+a_{16})16}{2}=\frac{(48+3)16}{2}$=408

Ответ: сумма положительных членов арифметической прогрессии равна 408.

Найти разность прогрессии
Создано: @nick 23 июля 2016 15:34
поставьте оценку:
1 голосов, средний бал: 5.0000

Дано: арифметическая прогрессия

$n$20
$n_{чет}$10
$n_{нечет}$10
$S_{n_{чет}}-S_{n_{нечет}}$80
$d$?

Сумма арифметической прогрессии $S_{n}=\frac{1}{2}(a_{1}+(a_{1}+d(n-1)))n$

Или $S_{1...20}=a_{1}+(a_{1}+d)+(a_{1}+2d)+(a_{1}+3d)+(a_{1}+2d)+...+(a_{1}+19d)$

Для нечетных номеров

$S_{1...19}=a_{1}+(a_{1}+2d)+(a_{1}+4d)+...+(a_{1}+18d)=10a_{1}+90d$
$S_{1...19}=10a_{1}+(2+4+6+8+10+12+14+16+18)d=90d$

Для четных номеров

$S_{2...20}=(a_{1}+d)+(a_{1}+3d)+(a_{1}+5d)+...+(a_{1}+19d)=10a_{1}+100d$
$S_{2...20}=10a_{1}+(1+3+5+7+9+11+13+15+17+19)d=90d$

$S_{2...20}-S_{1...19}=10a_{1}+100d-10a_{1}-90d=10d=80, откуда d$=8

Ответ: разность прогрессии равна 8.

Найти тангенс меньшего угла треугольника
Создано: @nick 23 июля 2016 07:21
поставьте оценку:
0 голосов, средний бал: 0.0000

Дано: треугольник, углы треугольника составляют арифметическую прогрессию

Меньший угол треугольника$α_{1}$
Средний угол треугольника$α_{2}$
Больший угол треугольника$α_{3}$75°
$tgα_{1}$=?

Решение: $S=α_{1}+α_{2}+α_{3}=180°, откуда α_{2}=180°-α_{1}-75°=105°-α_{1}$

Согласно определению арифметической прогрессии $α_{2}=α_{1}+d$

$α_{3}=α_{2}+d=105°-α_{1}+d=75°, откуда α_{1}=105°-75°+d=30°+d$

Сумма членов арифметической прогрессии $S=(30°+d)+((30°+d)+d)+(((30°+d)+d)+d)=90°+6d=180°, откуда d$=15°

$α_{1}=30°+15°=45°, и tg$45°=1

Ответ: тангенс меньшего угла треугольника равен 1.

Найти тангенс меньшего угла прямоугольного треугольника
Создано: @nick 22 июля 2016 12:56
поставьте оценку:
0 голосов, средний бал: 0.0000

Дано: углы прямоугольного треугольника

Меньший из двух острых углов$α_{1}$
Больший из двух острых углов$α_{2}$
Третий угол прямой или 90°$α_{3}$
$tgα_{1}$?

Сумма углов треугольника: $S=α_{1}+α_{2}+α_{3}$=180°, учитывая данные задачи $α_{1}+α_{2}$=90°, откуда $α_{2}=90°-α_{1}$

Арифметическая прогрессия это такая последовательность чисел, в которой разность между последующим и предыдущим членами прогрессии остается неизменной. Эта неизменная разность называется разностью прогрессии. $α_{2}=α_{1}+d$

$α_{3}=α_{2}+d$, в то же время по условиям задачи $α_{2}=90°-α_{1}$, тогда

$α_{3}=90°-α_{1}+d$=90°, откуда $α_{1}=d$, тогда

$S=α_{1}+α_{2}+α_{3}=α_{1}+(α_{1}+α_{1})+((α_{1}+α_{1})+α_{1})=α_{1}+2α_{1}+3α_{1}=6α_{1}$=180°, откуда $α_{1}=30°$

$tgα_{1}=tg30°=tg\frac{π×30°}{180°}=tg0,5236$=0,5773

Ответ: тангенс меньшего угла треугольника равен 0,5773.

Найти косинус угла
Создано: @nick 21 июля 2016 17:44
поставьте оценку:
0 голосов, средний бал: 0.0000

Дано: арифметическая прогрессия

$α_{1}$30°
$α_{2}$35°
$α_{55}$?
$cosα_{55}$?

Любой член арифметической прогрессии может быть вычислен по формуле $α_{n}=α_{1}+d(n-1)$

где $d=α_{n}-α_{n-1}=α_{2}-α_{2-1}=35°-30°=5°$, тогда

$α_{55}=30°+5°×(55-1)=300°, для того чтобы найти cosα_{55}=cos300°$ переведем градусы в радианы

$α_{55}=\frac{π×300°}{180°}$=5,236

$cosα_{55}=cos300°=cos5,236=\frac{1}{2}$

Ответ: $cosα_{55}=\frac{1}{2}$

Страницы:  12Следующие →
 Записать новую задачу Все задачи Все темы Все математики